Manning%27s Equation Excel Spreadsheet
- Google Sheets
- Manning 27s Equation Excel Spreadsheet Download
- Excel Free Download
- Free Manning's Equation Excel Spreadsheet
- Manning's Equation Excel Spreadsheet
- Manning Excel Sheet
A spreadsheet model that is based on solving Manning equation for wide channel cross-section assumption has been developed. The model shows the variation of the water level in the cross-section. Equations are also given for calculating the Manning roughness coefficient, n, for a given depth of flow in a pipe of known diameter. Numerous worked examples illustrate the use of these equations together with the Manning equation for partially full pipe flow. A spreadsheet for making partially full pipe flow.
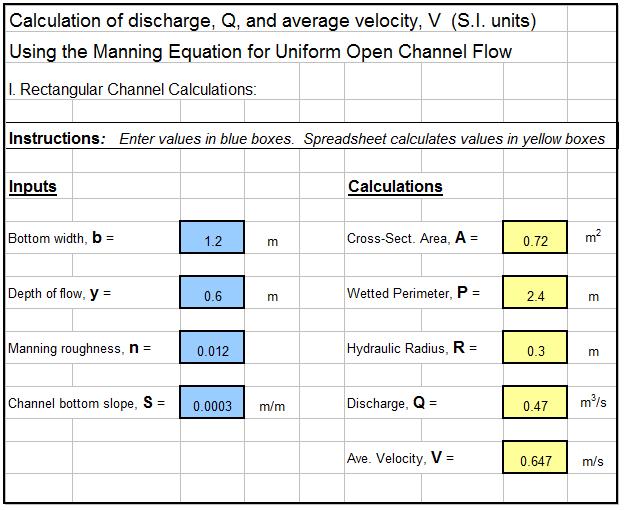
- The Manning equation, given below as Equation (1) and Equation (2), is the most widely used equation for uniform open channel flow calculations. Note that the Manning equation is a dimensional equation. That is, the U.S. Units given below must be used for the U.S. Version of the equation and the S.I. Units given below.
- Aug 16, 2010 The Excel spreadsheet formulas shown will then calculate the cross-sectional area of flow, the wetted perimeter, the hydraulic radius, and the Manning roughness coefficient. The image at the right shows the calculated results for a triangular channel with side slope of z = 3, bottom slope of S= 0.0003, flow depth of y = 2 ft, volumetric flow.
Where to Find Partially Full Pipe Flow Calculator Spreadsheets
To obtain Excel spreadsheets for partially full pipe flow calculations, click here to visit our spreadsheet store for partially full pipe flow calculator spreadsheets. Read on for information about Excel spreadsheets that can be used as a partially full pipe flow calculator.
The Manning equation can be used for flow in a pipe that is partially full, because the flow will be due to gravity rather than pressure. the Manning equation [Q = (1.49/n)A(R2/3)(S1/2) for (U.S. units) or Q = (1.0/n)A(R2/3)(S1/2) for (S.I. units)] applies if the flow is uniform flow For background on the Manning equation and open channel flow and the conditions for uniform flow, see the article, “Manning Equation/Open Channel Flow Calculations with Excel Spreadsheets.”
Direct use of the Manning equation as a partially full pipe flow calculator, isn’t easy, however, because of the rather complicated set of equations for the area of flow and wetted perimeter for partially full pipe flow. There is no simple equation for hydraulic radius as a function of flow depth and pipe diameter. As a result graphs of Q/Qfull and V/Vfull vs y/D, like the one shown at the left are commonly used for partially full pipe flow calculations. The parameters, Q and V in this graph are flow rate an velocity at a flow depth of y in a pipe of diameter D. Qfull and Vfull can be conveniently calculated using the Manning equation, because the hydraulic radius for a circular pipe flowing full is simply D/4.
With the use of Excel formulas in an Excel spreadsheet, however, the rather inconvenient equations for area and wetted perimeter in partially full pipe flow become much easier to work with. The calculations are complicated a bit by the need to consider the Manning roughness coefficient to be variable with depth of flow as discussed in the next section.
Is the Manning Roughness Coefficient Variable for Partially Full Pipe Flow Calculations?
Using the geometric/trigonometric equations discussed in the next couple of sections, it is relatively easy to calculate the cross-sectional area, wetted perimeter, and hydraulic radius for partially full pipe flow with any specified pipe diameter and depth of flow. If the pipe slope and Manning roughness coefficient are known, then it should be easy to calculate flow rate and velocity for the given depth of flow using the Manning Equation [Q = (1.49/n)A(R2/3)(S1/2)], right? No, wrong! As long ago as the middle of the twentieth century, it had been observed that measured flow rates in partially full pipe flow aren’t the same as those calculated as just described. In a 1946 journal article (ref #1 below), T. R. Camp presented a method for improving the agreement between measured and calculated values for partially full pipe flow. The method developed by Camp consisted of using a variation in Manning roughness coefficient with depth of flow as shown in the graph above.
Although this variation in Manning roughness due to depth of flow doesn’t make sense intuitively, it does work. It is well to keep in mind that the Manning equation is an empirical equation, derived by correlating experimental results, rather than being theoretically derived. The Manning equation was developed for flow in open channels with rectangular, trapezoidal, and similar cross-sections. It works very well for those applications using a constant value for the Manning roughness coefficient, n. Better agreement with experimental measurements is obtained for partially full pipe flow, however, by using the variation in Manning roughness coefficient developed by Camp and shown in the diagram above.
The graph developed by Camp and shown above appears in several publications of the American Society of Civil Engineers, the Water Pollution Control Federation, and the Water Environment Federation from 1969 through 1992, as well as in many environmental engineering textbooks (see reference list at the end of this article). You should beware, however that there are several online calculators and websites with equations for making partially full pipe flow calculations using the Manning equation with constant Manning roughness coefficient, n. The equations and Excel spreadsheets presented and discussed in this article use the variation in n that was developed by T.R. Camp.
Excel Spreadsheet/Partially Full Pipe Flow Calculator for Pipe Less than Half Full
The parameters used in partially full pipe flow calculations with the pipe less than half full are shown in the diagram at the right. K is the circular segment area; S is the circular segment arc length; h is the circular segment height; r is the radius of the pipe; and θ is the central angle.
The equations below are those used, together with the Manning equation and Q = VA, in the partially full pipe flow calculator (Excel spreadsheet) for flow depth less than pipe radius, as shown below.
- h = y
- θ = 2 arccos[ (r – h)/r ]
- A = K = r2(θ – sinθ)/2
- P = S = rθ
Google Sheets
The equations to calculate n/nfull, in terms of y/D for y < D/2 are as follows
- n/nfull = 1 + (y/D)(1/3) for 0 < y/D < 0.03
- n/nfull = 1.1 + (y/D – 0.03)(12/7) for 0.03 < y/D < 0.1
- n/nfull = 1.22 + (y/D – 0.1)(0.6) for 0.1 < y/D < 0.2
- n/nfull = 1.29 for 0.2 < y/D < 0.3
- n/nfull = 1.29 – (y/D – 0.3)(0.2) for 0.3 < y/D < 0.5
The Excel template shown below can be used as a partially full pipe flow calculator to calculate the pipe flow rate, Q, and velocity, V, for specified values of pipe diameter, D, flow depth, y, Manning roughness for full pipe flow, nfull; and bottom slope, S, for cases where the depth of flow is less than the pipe radius. This Excel spreadsheet and others for partially full pipe flow calculations are available in either U.S. or S.I. units at a very low cost in our spreadsheet store.
Excel Spreadsheet/Partially Full Pipe Flow Calculator for Pipe More than Half Full
The parameters used in partially full pipe flow calculations with the pipe more than half full are shown in the diagram at the right. K is the circular segment area; S is the circular segment arc length; h is the circular segment height; r is the radius of the pipe; and θ is the central angle.
The equations below are those used, together with the Manning equation and Q = VA, in the partially full pipe flow calculator (Excel spreadsheet) for flow depth more than pipe radius, as shown below.
- h = 2r – y
- θ = 2 arccos[ (r – h)/r ]
- A = πr2 – K = πr2 – r2(θ – sinθ)/2
- P = 2πr – S = 2πr – rθ
The equation used for n/nfull for 0.5 < y//D < 1 is: n/nfull = 1.25 – [(y/D – 0.5)/2]
An Excel spreadsheet like the one shown above for less than half full flow, and others for partially full pipe flow calculations, are available in either U.S. or S.I. units at a very low cost at www.engineeringexceltemplates.com.
References
1. Bengtson, Harlan H., Uniform Open Channel Flow and The Manning Equation, an online, continuing education course for PDH credit.
2. Camp, T.R., “Design of Sewers to Facilitate Flow,” Sewage Works Journal, 18 (3), 1946
3. Chow, V. T., Open Channel Hydraulics, New York: McGraw-Hill, 1959.
4. Steel, E.W. & McGhee, T.J., Water Supply and Sewerage, 5th Ed., New York, McGraw-Hill Book Company, 1979
5. ASCE, 1969. Design and Construction of Sanitary and Storm Sewers, NY
6. Bengtson, H.H., “Manning Equation Partially Filled Circular Pipes,” An online blog article
7. Bengtson, H.H., “Partially Full Pipe Flow Calculations with Spreadsheets“, available as an Amazon Kindle e-book and as a paperback.
Where to find Excel Spreadsheets for Watershed Time of Concentration
To obtain an Excel spreadsheet for watershed time of concentration calculations, click here to visit our spreadsheet store. Obtain a convenient, easy to use spreadsheet for watershed time of concentration calculation at a reasonable price. Read on for information about Excel spreadsheets that can be used for watershed time of concentration calculations.
The time of concentration for a watershed is the time for rainfall that lands on the farthest point of the watershed to reach the outlet. The main reason for interest in the watershed time of concentration is for its use as the storm duration in finding the design rainfall intensity to use in Rational Method calculation of peak storm water runoff rate.
The reason that the watershed time of concentration is used as design storm duration is because it gives the largest peak storm water runoff rate for a given return period. This can be reasoned out as follows: If the storm duration is less than the time of concentration, then the storm will end before runoff from the entire watershed reaches the outlet. Thus flow from the entire watershed will never all be contributing to the outflow. If the storm duration is greater than the time of concentration, then the storm will continue longer than it takes for the entire watershed to contribute to the outflow, but the storm intensity will be less for a storm of longer duration than one of short duration for a given return period. Thus the maximum peak storm water runoff rate for a specified return period on a given watershed will be for a storm with duration equal to the time of concentration of that watershed.
We can now move on to a discussion of how to calculate values for the time of concentration of a given watershed.
Methods for Estimating Watershed Time of Concentration
There are several empirical equations that have been developed for calculating travel time/time of concentration for different types and conditions of watersheds. Some examples are the Kerby equation, the Izzard equation, the Manning Kinematic equation, the Bransby Williams equation, the National Resources Conservation Service (NCRS) method, and the Manning equation. The following three equations will be discussed in this article: 1) the Manning Kinematic equation for use with overland sheet flow, 2) the NRCS method for shallow concentrated flow, and 3) the Manning equation for channel flow. These three methods are recommended by the U.S. Soil Conservation Service (SCS) in ref #1 at the end of this article. The Iowa Stormwater Management Manual (ref #2) also recommends these three methods. Typically overland sheet flow will occur in the upper portion of the watershed, followed by shallow concentrated flow, with channel flow for the final portion of watershed before the outlet.
Calculations with the Manning Kinematic Equation
The boxes at the right show the Manning Kinematic equation for U.S. and for S.I. units. The parameters in the Manning Kinematic equation and their units are as follows:
- t1 = overland sheet flow runoff travel time, min (NOTE: many places show the constant being 0.007 for U.S. units giving the time in hours. The equations in the boxes both give travel time in minutes.)
- n = Manning roughness coefficient, dimensionless*
- L = length of flow path, ft (S.I. – m)
- P = 2 year, 24 hr rainfall depth, in (S.I. – m)
- S = ground slope, ft/ft (S.I. m/m)
*See table of n values below.
The screenshot of an Excel spreadsheet template shown below will calculate overland sheet flow travel time with U.S. units using the Manning kinematic equation, based on the input values entered for the other parameters listed above. A tables with values of the Manning roughness coefficient for various overland flow conditions is also given below. This Excel spreadsheet and others for time of concentration calculations are available in either U.S. or S.I. units at a very low cost in our spreadsheet store.
Manning 27s Equation Excel Spreadsheet Download
Watershed Time of Concentration Calculations with the NRCS Method
The Manning Kinematic equation is recommended for travel length of no greater than 300 ft in ref #1 and for no greater than 100 ft in ref #2. Both of these references recommend use of the NCRS method for the shallow concentrated flow that normally develops within 100 to 300 ft into the watershed. The NCRS method calculates the velocity of the shallow concentrated flow first, based on the slope and the type of surface. The travel time is then calculated as travel length divided by velocity of flow. The equations used for the NRCS method are:
- t2= L/(60V) ( for either U.S. or S.I. units )
- V = 16.1345 S0.5 for U.S. units ( V = 4.9178 S0.5 for S.I. units) for an unpaved surface
- V = 20.3282 S0.5 for U.S. units ( V = 6.1960 S0.5 for S.I. units) for a paved surface
Excel Free Download
An explanation of each of the parameters used in these equations follows:
- L is the length of the flow path in ft for U.S. or m for S.I. units
- V is the velocity of flow in ft/sec for U.S. or m/s for S.I. units
- S is the slope of the flow path, which is dimensionless for either U.S. or S.I. units
- t2 is the travel time for shallow concentrated flow in minutes (for either U.S. or S.I. units)
The screenshot of an Excel spreadsheet template shown at the left will calculate shallow concentrated flow travel time with S.I. units using the NRCS method, based on the input values indicated. This Excel spreadsheet and others for time of concentration calculations are available in either U.S. or S.I. units at a very low cost at www.engineeringexceltemplates.com or in our spreadsheet store.
Calculation of Travel Time with the Manning Equation
The Manning equation is used for quite a variety of open channel flow calculations. It is recommended in ref#1 and ref #2 for any channel flow portion of the watershed runoff path. The following equations are used for Manning equation calculations:
- The Manning equation in U.S. units: Q = (1.49/n)A(R2/3)(S1/2)
- The Manning equation in S.I. units: Q = (1.0/n)A(R2/3)(S1/2)
- R = A/P
- V = Q/A
- t3= L/(60V)
An explanation of the parameters in these equations and their U.S. and S.I. units follows:
- Q = channel flow rate in cfs for U.S. units or m3/s for S.I. units
- V = average velocity of flow in ft/sec for U.S. units or m/s for S.I. units
- R = hydraulic radius of the channel (= A/P) in ft for U.S. units or m for S.I. units
- A = channel cross-sectional area in ft2 for U.S. units or m2 for S.I. units
- P = wetted perimeter of channel in ft for U.S. units or m for S.I. units
- S = channel bottom slope, which is dimensioness for either set of units
- n = Manning roughness coefficient for channel
- L = length of flow path in ft for U.S. units or m for S.I. units
- t3 = travel time for channel flow in min for either set of units
The screenshot of an Excel spreadsheet template shown at the right will calculate channel flow travel time with U.S. units using the NRCS method, based on the input values indicated. This Excel spreadsheet and others for time of concentration calculations are available in either U.S. or S.I. units at a very low cost at www.engineeringexceltemplates.com or in our spreadsheet store.
Free Manning's Equation Excel Spreadsheet
The overall time of concentration can now be calculated as the sum of t1, t2 and t3.
Manning's Equation Excel Spreadsheet
References:
Manning Excel Sheet
1. U.S. Soil Conservation Service, Technical Note – Hydrology No N4, June 17, 1986.
2. Iowa Stormwater Management Manual, Section on Time of Concentration.
3. Knox County Tennessee Stormwater Management Manual, section on the Rational Method.
4.Bengtson, Harlan H., Hydraulic Design of Storm Sewers, Including the Use of Excel, an online, continuing education course for PDH credit.
5. Bengtson, Harlan H., “Spreadsheets for Rational Method Hydrological Calculations,” an Amazon Kindle e-book.